Równanie sztywne

Równania sztywne – równania różniczkowe, dla których rozwiązania niektórymi metodami numerycznymi są niestabilne, chyba że zastosuje się ekstremalnie mały kroku całkowania. Dokładne określenie warunków, pozwalających przewidzieć, które równania różniczkowe należą do klasy równań sztywnych, nastręcza trudności. Jednak wyróżnikiem jest, że równania sztywne zawierają człony, które mogą prowadzić do szybkiej zmiany w rozwiązaniu. Jedna z pierwszych metod numerycznych przeznaczonych do tych równań została opisana przez K.C. Sparka.

Przykład

Ilustracja rozwiązań problemu opisanego w tekście

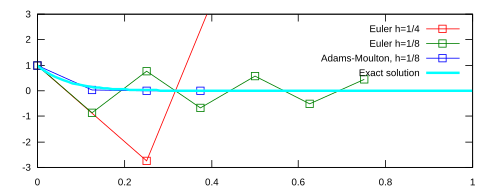
Rozważmy następujące zagadnienie początkowe:

$y'(t)=-15y(t),\quad t\geqslant 0,y(0)=1.$

Rozwiązanie analityczne (kolor sinoniebieski na wykresie) jest następujące:

$y(t)=e^{-15t},$ $y(t)\to 0$ dla $t\to \infty .$

Rysunek po prawej prezentuje rozwiązania przy użyciu trzech różnych metod:

1. Metoda Eulera z krokiem $h=1/4$ daje w rozwiązaniu duże oscylacje (kolor czerwony).
2. Metoda Eulera z dwukrotnie mniejszym krokiem, $h=1/8,$ generuje rozwiązanie o mniejszych oscylacjach (kolor zielony).
3. Metoda trapezów daje najlepsze rozwiązanie, zbiegające do zera (kolor niebieski).

Zobacz też

• sztywny układ równań
• wskaźnik uwarunkowania
• zagadnienie poprawnie postawione